A monopsony is illustrated in Figure 2:

Figure 2. A monopsony

As in Figure 1, the number of workers, N, is measured along the horizontal axis, while wage rates and the value of the product of labor are measured vertically. In contrast to the competitive market, there is only one employer in this market, so there is no labor demand schedule, per se. However, the employer does have a falling value of marginal product (VMP) schedule which, as in the competitive model, reflects the diminishing marginal productivity of labor. The labor supply schedule is given by the wage function w(N) which, as in the competitive model, indicates the minimum wage that would have to be paid in order to hire N workers.

The upward-sloping function C'(N), which was not present in the competitive model illustrated in Figure 1, represents the marginal factor cost of labor — the cost of hiring the incremental worker. For an individual employer in a competitive labor market, the marginal factor cost is simply the wage rate; the firm is too small relative to the size of the market to affect the level of wages. A monopsonist, however, is large enough relative to his market that his hiring decisions will cause wages to move up or down. The more workers he hires, the higher the wage he will have to pay, and assuming he pays the same wage to all of his employees, this means that the marginal factor cost at a given level of employment has to be higher than the wage rate.

This is best explained by a simple example. Suppose the wage function is w(N) = 10 + N, and suppose the employer is trying to decide whether to hire five or six workers. If he hires five workers the wage rate will be w(5) = 10 + 5 = $15, and his total wage bill will 5 * w(5) = $75. If he hires six workers, the wage rate will be w(6) = 10 + 6 = $16, and the total wage bill will 6 * w(6) = $96. The marginal factor cost of the sixth worker is not the wage rate, but the difference in total labor costs, i.e. $96 – $75 = $21.

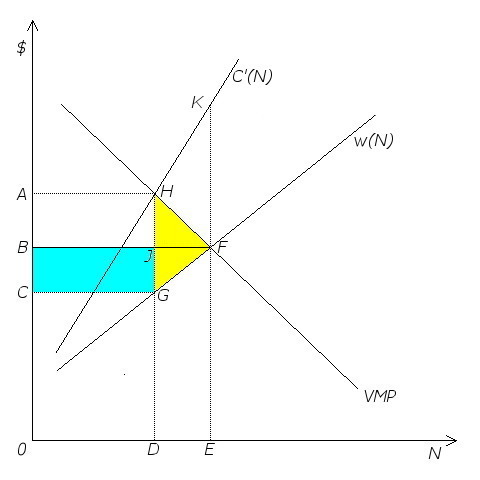
The monopsonist’s optimal level of employment is at the point at which the value of the marginal product of labor is equal to the marginal factor cost. This occurs at point H in Figure 2, where 0D workers are hired. The marginal factor cost at that level of employment is 0A, but the wage actually paid to workers is 0C, the height of the wage function w(N) when 0D workers are employed.

Employment level 0D, while optimal from the employer’s point of view, is socially inefficient in that the total surplus could be increased if more than 0D workers were employed. Recall that in the competitive model, total surplus was the area between the labor supply and demand curves to the left of the employment level. Here it is the area between the labor supply and VMP curves to the left of the employment level. As shown in Figure 2, workers’ surplus is the area above the wage schedule, w(N), and below the line CG. The employer’s share of the surplus is the area above CG and below the VMP schedule to the left of the vertical line HG.

Bilateral monopoly

Now assume a union comes in and negotiates a minimum wage of 0B. The result of this is that the labor supply curve now facing the employer is the horizontal line running from point B on the vertical axis to point F, after which it is identical with the original labor supply curve w(N). Since the employer must pay a wage of at least 0B to hire up to 0E workers, the marginal factor cost up to that level of employment is identical with the new labor supply curve — the horizontal line running from B to F. However, there is a discontinuity at point F and if the employer hires more than 0E workers, the marginal factor cost is given by the original C'(N) function. Facing these new conditions, the monopsonist will hire 0E workers, all of whom will be paid the union wage 0B.

Notice that as a result of the union contract, both the wage rate and the level of employment have risen. Notice also that the total surplus has increased by an amount represented by the yellow-shaded triangle, GHF. This expanded surplus is shared by workers and their employer, with workers getting GJF and their employer getting JHF. In addition, some surplus, represented by the turquise-shaded rectangle CBJG, has been redistributed from the employer to his workers.

Most analyses of bilateral monopoly — the term used to describe markets in which a single buyer (the employer) is negotiating with a single seller (the union) — either stop at this point or suggest that bargaining will produce a wage somewhere between 0C and 0A. Any wage in that range will increase both the wage rate and the total surplus, and the presumption is that the two parties only disagree on how to divide this gain.

Actually, there is no reason to presume that a union facing a single employer will try to negotiate a wage that increases the total surplus. This presumption is a result of the erroneous view of a trade union as a single, self-interested entity driven by the same profit-maximization impulses that motivate the employer. As I argued previously in the discussion of competitive labor markets, a union does not seek to maximize the total income of all the workers in its craft or industry, but the welfare of a majority of its members.